Using manual ticks
Introduction: Manual tick positions
Manual tick and labels positioning is used to have absolute full control over the placement of ticks (both major and minor) as well as the labels. The ticks can be arbitrary placed over the entire scale of the axis. This feature is of course applicable to both the X and Y axis.
In this short article we will give two example to illustrate how this feature can be used.
In the first example we assume that the X-axis are timestamps and the manual tick positioning are used to label the exact start of each month. The normal date scale (which uses the standard ticks) can not be used for this purpose since the ticks are placed at even intervals. Since the length of the months are not equal this makes it impossible to have ticks at exactly the start of the month.
In the second example we show how this feature can be used to put labels at zero crossings of a sinus where the labels show multiples of Pi.
Date scale with timestamp
The first example shows a very common use case where the X-axis have the unit of timestamps and the start of each month is labeled. This is difficult (impossible) to do with the automatic tick marks since this requires the distance between consequitive tick marks to be different. Figure 1 shows a basic example of what can be expected.
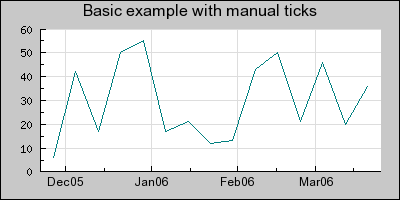
Figure 1. Labels positioned at the very start of each month, note the added "grace" in the beginning and end of the X-scale to avoid any labels overshooting the end (or the start) of the X-axis.
To use the manual tick marks two steps are required
- Determine where the tick marks should be. Both major (which can have a label and grid marks) and minor ticks can be specified. Optionally if complex labels, which cannot be calculated by a format string (either as date or printf() format) needs needs to be created.
- Call the appropriate method to set the tick marks and optional labels.
Useful methods to work with manual tick marks
The following methods (in class Axis) are available to set the tick marks
Axis::SetTickPositions($aMajTickPos,$aMinTickPos=NULL,$aLabels=NULL)Axis::SetMajTickPositions($aMajTickPos,$aLabels=NULL)
The second method above is strictly speaking not necessary, it is just a convenience function for those cases where only major ticks and labels should be set.
The following related method will also be used in this example
Axis::SetLabelFormatString($aFormat,$aIsDateFormat=FALSE)
This method has been available for a long time in the library but it has recently gained the second argument. With this argument it is possible to tell if the formatting string should be interpretated as format according to the standard printf() format or if it should be interpretated as a format string to be used with the date() function.
Finally we will use a utility function that is available in (from ver 1.20 of the library) jpgraph_utils.inc
DateScaleUtils::GetTicks($aData,$aType==DSUTILS_MONTH1)
Possible values for the second argument are
- DSUTILS_MONTH1. Return an array with major and minor ticks on a monthly basis. The minor ticks are set at the middle of the month.
The GetTicks() is a utility function that given an array of timestamps returns an array of major and minor tick mark positions that marks the start and middle of each month.
Putting it all together
To make the graph in figure 1 we first note that it is probably a good idea to specify the min and max value of the X-axis ourself rather than letting the autoscale algorithm do that. Since the timestamps are possibly quite large values and the autoscaling algorithm will try to make the start and end values be "even" (for example multiples of 5,10,100, .. and so on).
Secondly we need to chose what scale we will use. In this case it doesn't really matter if we chose a integer (int) or a linear (lin) scale. But since timestamps by definition are integers we select an int scale for the X-axis.
Finally we need to decide what format to have on the labels. For this example we chose to show it as "Dec05" to indicate "December 2005". The format string needed to select this is "My" which we will use as argument for the SetLabelFormatString() method. Since the width of the label is medium wide we add some empty space on each side of the graph after we positioned the ticks to avoid the first label "hitting" the Y-axis labels. This could happen if the start of the first month on the axis is very near the X-Y axis conjunction.
We will now walk through the code to create the image in Figure 1 and explain each step.
First we create some random data for the X and Y axis
$datay = array();
$datax = array();
$ts = time();
$n=15; // Number of data points
for($i=0; $i < $n; ++$i ) {
$datax[$i] = $ts+$i*700000;
$datay[$i] = rand(5,60);
}
Then we get the tick positions for the start of the months
list($tickPositions,$minTickPositions) = DateScaleUtils::GetTicks($datax);
We also add a bit of space "grace value" at the beginning and end of the axis
$grace = 400000; $xmin = $datax[0]-$grace; $xmax = $datax[$n-1]+$grace;
It is now time to add the standard code to setup a basic graph. We also set the previously calculated tick positions and the label formatting string we want to use.
Note that we are careful at making sure the X-axis always start at the minimnum Y-value (by calling SetPos() ), by default the X-axis is otherwise positioned at Y=0 and if the Y-scale happens to start at, say Y=10, then the X-axis is not shown.
$graph = new Graph(400,200);
$graph->SetScale('intlin',0,0,$xmin,$xmax);
$graph->title->Set('Basic example with manual ticks');
$graph->title->SetFont(FF_ARIAL,FS_NORMAL,12);
$graph->xaxis->SetPos('min');
$graph->xaxis->SetTickPositions($tickPositions,$minTickPositions);
$graph->xaxis->SetLabelFormatString('My',true);
$graph->xaxis->SetFont(FF_ARIAL,FS_NORMAL,9);
$graph->xgrid->Show();
Finally we create and add the plot to the graph and send back the graph to the browser.
$p1 = new LinePlot($datay,$datax);
$p1->SetColor('teal');
$graph->Add($p1);
$graph->Stroke();
The complete source of this example is available in the Examples directory as "manualtickex1.php"
Using manual labels
In the example we walked through above we used a formatting string to automatically create the labels. As we also noted above it is perfectly possible to use fully manual labels. We now show an example of this and put labels at irrational intervals.
In this example we create a very simple sinus-like curve and add labels at multiples of 1/2 Pi.

Figure 2. The function "cos(t) + 3/2*cos(2t)" plotted with labels at 1/2 PI intervals.
In order to create this graph we used the methods as described above with a manually constructed label array. In order to create the labels easily we also made use of one utility Class SymChar (available in jpgraph_utils.inc) that gives easy access to Greek characters, like the PI sign we use in the labels. The usage of this utility is further described in "HowTo: Greek Characters"
Putting it all together
Let's now walk through the script needed to create this graph. To create the actual function plot we used another utily, the FuncGenerator class that given a function calculates a suitable number of X,Y coordinates to draw the function graph.
Note: The string passed to the function generator is evaluated as a PHP statement. This means that a client should never pass arbitrary functions or unchecked data, especially not unchecked data from a WEB-application, since it is a potential huge security risk which could allow code injection on a server!
$f = new FuncGenerator('cos($x)+1.5*cos(2*$x)');
list($datax,$datay) = $f->E(0,10);
We should now create the labels and the tick positions. We put them at intervals of 1/2 PI.
$tickPositions = array();
$tickLabels = array();
$tickPositions[0] = 0;
$tickLabels[0] = '0';
for($i=1; $i/2*M_PI < 11 ; ++$i ) {
$tickPositions[$i] = $i/2*M_PI;
if( $i % 2 )
$tickLabels[$i] = $i.'/2'.SymChar::Get('pi');
else
$tickLabels[$i] = ($i/2).SymChar::Get('pi');
}
As usual we want to make sure that the scale of the X-axis covers our function exactly so we need to find out the min and max values along the X-axis and use them to manually set the scale.
$n = count($datax); $xmin = $datax[0]; $xmax = $datax[$n-1];
It's now time to setup the basic graph. This is very similair to waht we did before with the only difference that we use the SetMajtickPosition() method to avoid a NULL argument for the minor ticks which we are not interested in.
$graph->SetScale('linlin',0,0,$xmin,$xmax);
$graph->title->Set('Example with manual tick labels');
$graph->title->SetFont(FF_ARIAL,FS_NORMAL,12);
$graph->xaxis->SetPos('min');
$graph->xaxis->SetMajTickPositions($tickPositions,$tickLabels);
$graph->xaxis->SetFont(FF_TIMES,FS_NORMAL,10);
$graph->yaxis->SetFont(FF_TIMES,FS_NORMAL,10);
$graph->xgrid->Show();
and finally we add the plot to the graph
$p1 = new LinePlot($datay,$datax);
$p1->SetColor('teal');
$graph->Add($p1);
The complete source of this example is available in the Examples directory as "manualtickex2.php"